3D Medusa

Multi-Digit Coloring Through Bi-Value Cells

By Minimal Sudoku Team•Last updated: February 19, 2026

Simple Coloring assigns two colors to one digit along chains of cells. 3D Medusa extends this by connecting different digits through bi-value cells, building larger coloring networks and unlocking eliminations that single-digit coloring cannot find.

⚡Quick Summary

What: Color candidates across multiple digits using two alternating colors
New link: Bi-value cells (exactly 2 candidates) bridge between digits
Result: Eliminations (kill trapped candidates) or contradictions (solve entire color)

How It Works

🎯 The Coloring Principle

Assign two colors (blue and green) to candidates along strong links — connections where exactly one of two options must be true. Because every link alternates, all candidates of one color are simultaneously true. We just don't know which color yet.

The chain uses two types of strong link:

Bi-location: A digit appears in exactly 2 cells in a row, column, or box. One must be true, the other false → opposite colors.
Bi-value: A cell has exactly 2 candidates. One must be true, the other false → opposite colors. This is the “3D” bridge that lets the chain jump between digits.

A bi-value cell bridges between digit 3's chain and digit 9's chain.

To build a chain: pick any candidate on a strong link, color it blue, color the other end green, and keep following all strong links (both bi-location and bi-value), alternating colors until no more links remain. Then check for eliminations and contradictions.

Elimination

🎯 Dual-Color Elimination

An uncolored candidate can be eliminated if it would be removed regardless of which color is true.

For each uncolored candidate, ask two questions:

Would blue kill it? Yes if: a blue peer has the same digit (external), or the same cell has blue on any digit (internal).
Would green kill it? Same logic with green.

If both answers are yes, the candidate is dead no matter what. Eliminate it.

Example: Elimination

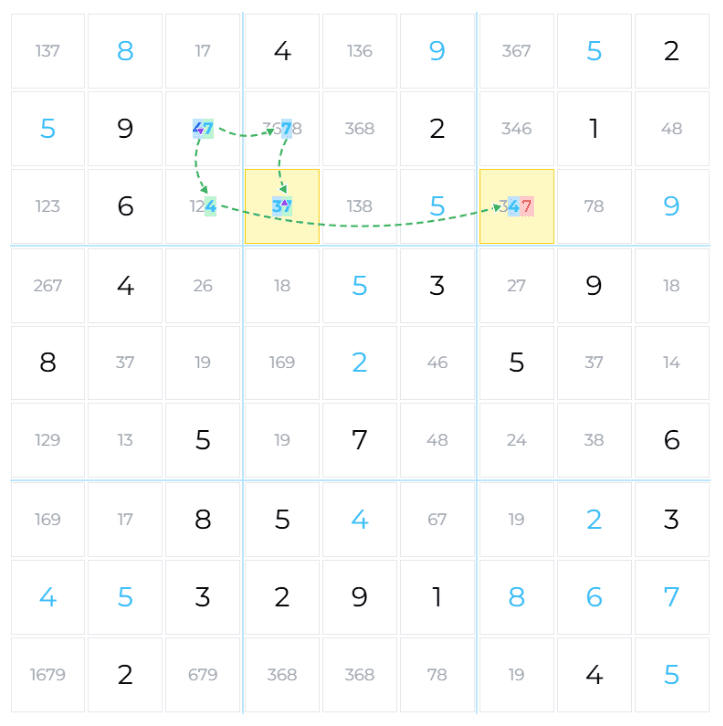
Let's walk through a real example. Focus on the top-left area of this board:

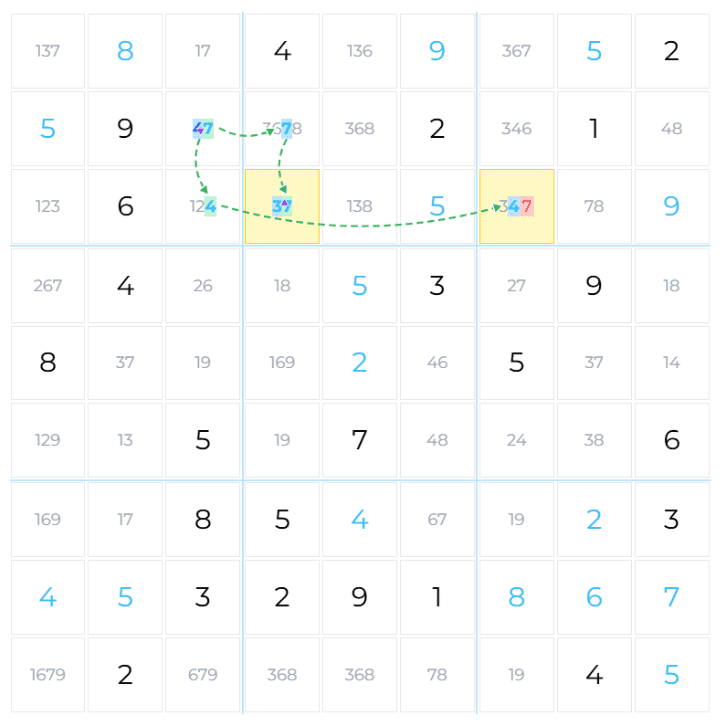
3D Medusa dual-color elimination example showing a 7-node chain across digits 4, 7, and 3

The chain spans 5 cells and 3 digits. The yellow cells directly cause the elimination.

Step 1: Start at a bi-value cell

Cell R2C3 has exactly two candidates: 4 and 7. Color 4 blue and 7 green. (The choice is arbitrary.)

Step 2: Build the chain

From R2C3, the chain branches into two paths:

Path A — digit 4

1.🔵 4 at R2C3 → only 2 cells for 4 in column 3 → 🟢 4 at R3C3

2.🟢 4 at R3C3 → only 2 cells for 4 in row 3 → 🔵 4 at R3C7

Path B — digit 7

3.🟢 7 at R2C3 → only 2 cells for 7 in row 2 → 🔵 7 at R2C4

4.🔵 7 at R2C4 → only 2 cells for 7 in column 4 → 🟢 7 at R3C4

5.🟢 7 at R3C4 → R3C4 has only {3, 7} → 🔵 3 at R3C4(bi-value bridge!)

The chain has 7 colored candidates across 5 cells and 3 digits. No contradictions found — check for eliminations.

Step 3: Find the elimination

Cell R3C7 has candidates {3, 4, 7}. Candidate 4 is colored (🔵 blue), but 7 is uncolored. Can both colors kill it?

If 🔵 blue is true:🔵 4 at R3C7 gets placed → 7 is removed.7 dies.

If 🟢 green is true:🟢 7 at R3C4 gets placed → same row, so 7 is removed from R3C7.7 dies.

Either way, candidate 7 cannot survive. Eliminate it. R3C7 is reduced to {3, 4}.

Why this example matters

Notice how the two paths converge: Path A colors the internal threat (blue 4 in the same cell), Path B colors the external threat (green 7 in the same row). Together, the candidate has no escape.

Contradiction

🎯 Contradiction

If one color leads to an impossible board state, that color is false. Solve every candidate of the true color and eliminate every candidate of the false color.

A color contradicts itself if any of these occur:

Same color twice in a cell

The cell would need two values — impossible.

Same color + digit twice in a unit

The unit would contain a duplicate — impossible.

An uncolored cell emptied

Every candidate in a cell would be eliminated — impossible.

Contradictions are rarer than eliminations but far more powerful — they can solve dozens of cells in one move.

Example: Contradiction

This example shows the immense power of a contradiction. The chain spans 47 colored candidates connected by 73 links — far too large to build by hand, but the solver handles it automatically.

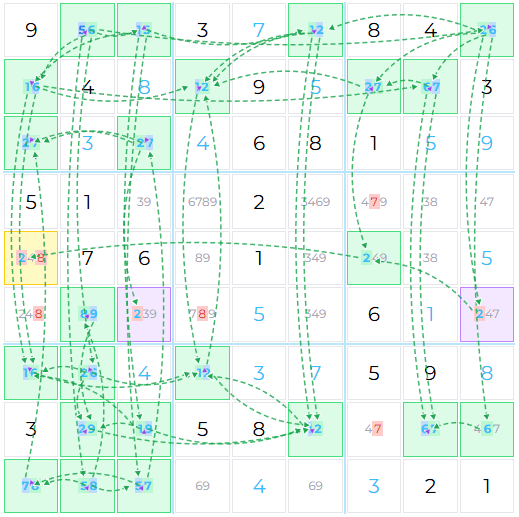
3D Medusa contradiction example showing a 47-node chain where blue is proven false

Purple cells: the contradiction. Green candidates: solved. Red candidates: eliminated.

The contradiction

Digit 2 appears as 🔵 blue in two cells in the same row:

🟪 R6C3contains 🔵 2

🟪 R6C9contains 🔵 2

Both in row 6. If blue were true, row 6 would have digit 2 twice — impossible.

The payoff

Blue is false, so 🟢 green is true. Every green candidate is solved, every blue candidate is eliminated: 23 cells solved in one move.

Best left to the solver

You won't build a 47-node chain by hand. Elimination on smaller chains is what you'll encounter most often. But when the solver finds a contradiction, the payoff is spectacular.

Tips

Start from Simple Coloring. Build single-digit chains first, then look for bi-value cells that bridge to other digits.
Check contradictions before eliminations. Contradictions are far more powerful — always check for them first.
Only use strong links. A unit with 3+ cells for a digit has no bi-location link. A cell with 3+ candidates has no bi-value link.

Relationship to traditional rules

You may see 3D Medusa described with six separate rules. Our Contradiction rule covers the traditional Rules 1, 2, and 6. Our Elimination rule covers Rules 3, 4, and 5. Same logic, simpler framing.

Simple Coloring is a special case of 3D Medusa where no bi-value links are used. If the chain stays on one digit, you are effectively doing Simple Coloring.

Advanced

Simple Coloring

Master single-digit coloring before tackling 3D Medusa.

Related Techniques

🔄X-Cycle 🔗XY-Chain ⛓️Alternating Inference Chains